Bioconductor之affy中quantiles normalization(分位数标准化)方法的介绍
quantiles标准化,也就是我将要介绍的最后一个标准化方法,这个标准化方法显然是顾名思义就是根据分位数进行标准化。
该算法在Bioconductor包内的preprocessCore包内,并且是由C语言实现的。
其调用方法也是非常的简单,第一个参数当然是源数据,第二个参数是选择对哪些部分进行标准化。
![]()
这个方法的第二个参数不同于之前的算法,例如我们传入pmonly时,是只对pm数据进行标准化,而mm数据是没有标准化的!!
separate是指pm和mm分开进行标准化,也就是pm在pm数据中标准化而mm在mm数据中标准化,together当然是一起标准化了。
在源码之中,整个算法分为两个部分,
ps,我发现这个算法和分位点也没什么关系啊,我首先介绍最简单的一种情况:
第一个部分,选择分位点:
这一部分就很奇怪,与其说分位点,不如说就是平均数,我首先介绍不存在Na的情况。在这一部分,首先是将每一列排个序,排序之后就除以列数求出一个平均值,然后将每一列的平均值相加。所以得到一个大小为行数,其值是每一列数据排序后除以列数相加。所以看起来也不是普通的平均值,而是排序之后的平均值,在代码里称为target。
这个是原数据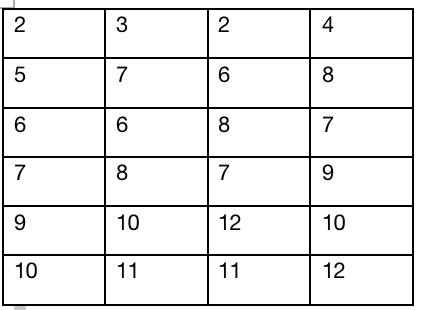 这个是排序完之后
这个是排序完之后
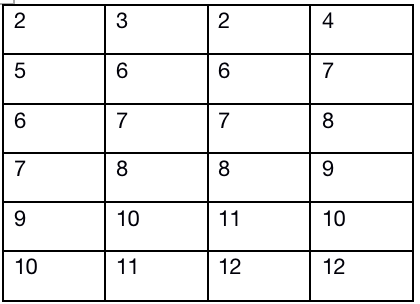 排序之后每一列相加求平均
排序之后每一列相加求平均

第二个部分,标准化:
上一部分我们得到一个target,然后我们将原数据每一行进行复制后排序,同时记录排序前的位置,并把排序后的位置称为rank。把target的rank位置的数直接赋给原数据,然后就完成标准化了。
然后根据原数据的位置把数据填进去。
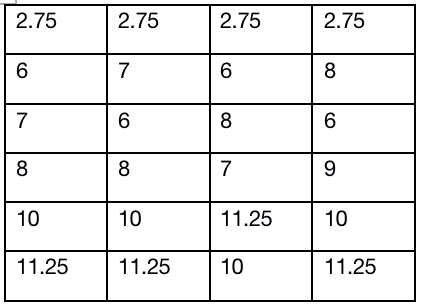
以上就是最最最简单的情况,会发现这个和RMA算法的标准化是一样的。是的RMA算法就是使用了quantiles标准化!!!
所以其有效性我就不重复分析了,这个算法还是非常有意义的。
当然我这篇文章肯定不会又在重复这种算法,接下来我要介绍这个算法是怎么处理NA数据的,同时在我上面的例子里rank不用再修改,因为没有相同的值,而这个在原算法里也是有特殊的处理方式的。
有了上面说了最最简单的情况,我们来考虑一下如果数据之中出现Na之后,也就是数据无效之后怎么处理:
整体的过程肯定是和上述是相同的,所以第一步还是求target,但是这一步出现了问题,因为如果有一列出现了Na,那么排序完,除去Na数据后,其行数是和其他列不同的,例如下面这种情况:
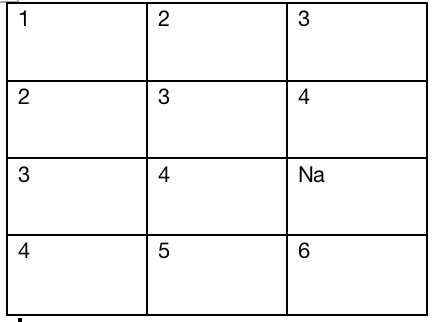
很显然,我已经排好序了,在这种情况里会发现少了一个数据。
但是我们所求的target肯定是要和总行数相同的。
那么我们就必须要考虑怎么样让3个数据的列能够变成4个数据以满足target的行数要求。
在算法里,是通过下列方式实现的:
首先我们得到该列非Na数据的个数记为N,并把Na数据存储于数组Narray,我们将矩阵行数记为Row,列数记为Col,我们要计算当前位置i的平均值。
将i/Row记为P,作为当前位置在总行数里面所占的百分位,也就是所谓的分位数标准化为什么取这个名字的本质所在。
将1 + (N - 1) * P记为index,因为我们知道N<Row,肯定是要求出这个位置在非Na数据的位置的百分位数,用这个百分位数经过一定的判定和计算后来求平均数。
因为double类型有精度问题,所以将接近整数的值就认为是整数,这个精度在代码里是通过一个叫做DOUBLE_EPS控制的。
也就是例如如下情况4*DOUBLE_EPS > |num - 4| 就认为num就等于4,可能看起来会很奇怪为什么要乘4,这个是源码的这么实现的,其实就算不乘4,乘以3也是可以的,这个就是一个精度问题。也就是说index如果接近整数,那么就把Narray[index]/Col 作为这个点的平均数
如果index刚好是整数,那肯定就更好了,都不用考虑精度问题,还是按照上述过程计算。
如果index是处于某两个整数a,b之间,先求出index离a的距离记为La,将(Narray[a] * La + Narray[b] * (1-La) )/Col也就是根据距离把两边的顶点按照比例相加作为平均数
那么通过上述方法,肯定是能将一个小于Row的数组映射成一个Row大小的数组,至此就解决了当出现Na时的target构建。
接下来就是使用target进行标准化了,还是同最最简单的情况一个思路,只不过要特殊处理一些相同的数据,
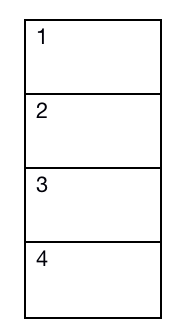
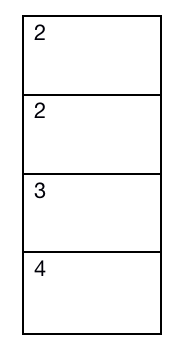 左侧是得到的target,右侧是原数据,很显然右侧出现了两个2,如果说这两个2一个标准化为1,一个标准化为2显然是非常不合理的。那么我们首先要解决这个问题。
左侧是得到的target,右侧是原数据,很显然右侧出现了两个2,如果说这两个2一个标准化为1,一个标准化为2显然是非常不合理的。那么我们首先要解决这个问题。
在源码里是按照如下过程实现的:
首先将某一列数据进行复制到一个新的数组Array,并且进行排序,排序后保存排序前的位置,也就是说我们的Array数据不仅仅保存了数据值也保存了当前下标i。
对Array进行一个循环假如说有连续相同的值,例如从下标i到下标j都是相同的值,那么Array[i:j]这些数据的下标都改为 1+(i + j) / 2, 并将新的下标重新保存到rank数组中
看rank的下标如果说是整数index,则把Array中取出排序前的位置,把这个位置的原数据用target[index]替代。
如果rank的下index标不是整数,则对index向下取整,将原数据用 (target[index] + target[index + 1]) / 2替代。
至此我们便考虑了原数据有相同数据值时的处理。
最后我们还要考虑原数据如果有Na时,该怎么处理标准化后的结果,这也是我们的最后一种特殊情况:
这个过程其实和target生成的过程很像,我就不进行大量重复的说明,我就说一些不同的地方。
我们知道target是将小于Row的数据扩展成Row的数据,而这里是将Row的数据反而变回小于Row行的数据,
所以我们那个百分位数求的不是i/Row了 而是i/N 也就这点区别,后面的也都是一样的。
因此这个算法其实原本是Na的数据后来还是Na,是不会改变的!!!!
说实话,这个算法写成这种博客还是很乱,不知道大家能不能看明白,如果还有问题可以留言。还是我功力不够,表达能力有限。
其实这个算法的源码不难理解,其中多线程的部分可以跳过,没什么意义,因为理解了单线程会发现多线程也没什么难度。
以及这个算法源码还有一个情况,就是目标行数是可以设置为小于总行数的,但是我觉得这种情况不会出现啊,就不多解释了,而且也没什么意义,只不过舍弃一些无用数据而已。
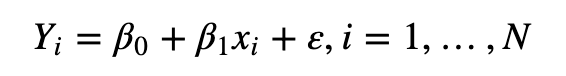



全部评论