网络上有很多关于PCA的文章，不得不说其实这个概念本身是不难的，然后网上就出现了很多各种各样的理解和解读，反而加大了大家对于这个概念的理解难度。
 

最近我发现生物信息学之中对于PCA的应用挺常见的，但是很多地方和我一开始理解的并不相同，为此，特地又去看了一遍PCA的推导。

这篇文章，我也是借鉴其他老师的思路而写，毕竟PCA这个东西已经有很长的历史了，所以肯定不是全网最好的。

但是我有信心我写的肯定是对的，因为这些公式我都自己推导过，和那些复制粘贴的有本质区别。

正文：

1，简单理解，PCA，是主成分分析，如上图这张非常经典的例子（我是从李宏毅老师ppt之中截图出来的，如果有版权问题，我立马修改），原来坐标之中是二维的，能不能在数据中找到一个新的方向，能够尽可能保留数据的信息，也就是只用一个维度(注意不是用原来的x轴或者y轴选一个，而是映射到新的一个方向)。在图片里，能够看到红色方向能够尽可能的体现点和点之间的关系，所以用红色以及和红色垂直的黄色基向量构成新的坐标空间，对于所有的点都映射到新的坐标上，再选择红色方向的坐标，就实现了降维。

举一个小例子：

如果说在原来坐标中有很多个点，其中三个为：(1,1) (2, 3) (3, 4)

也假设现在找到的新的基向量，在原坐标下基向量为, 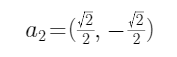可以简单看到，基向量是相互垂直切长度为1，

那么将点分别映射到新的坐标上，就是解方程：

得到的x和y就是新坐标系下的坐标，解得的结果就是

之后保留第一维即可，这样就实现了降维，我们用一维的信息就尽可能保留原来二维的信息了。

2，再前进一步

那么上面如果能够理解了，其实已经可以不用看下去了，因为下面是去找出来这个新的基向量，而原理和核心就是上面的部分了。

在这一步，我不太想和网络上大部分文章一样，一上来就搞一大推矩阵啊，然后网络上还有一大堆甚至于是错误的推导。

首先，将第一部分的内容公式化：

其中x是原来的数据，W是新的基向量，z就是新的空间上的某个基向量坐标，因为我们的x是一个数据集(这不是废话，如果x不是数据集也不用做PCA降维啊)，所以最后得到的z也是一个数据集。注意我这里有一个小标，因为对于n维空间，能找到n个新的相互垂直的单位向量构成新的空间，也就是得有n个W和n个z，每个新的基向量都有一个映射关系。

我们希望，映射后在z方向上尽可能保留原来坐标的信息，那就是要z方向上的数据集变化率要大，这个变化率的意思就是如最开始的图所示，红色方向数据变化大，黄色方向数据变化不大，那么红色就保留了更多的信息。所以我们要定义一个能够衡量这个变化率的东西：

也就是计算当前映射后数据集的均方差，如果说均方差很大不就说明数据的变化率很大吗。

其中有：

代会Var函数之中，得到：

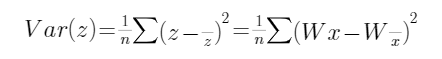
注意这里W是向量和x是矩阵，所以经过变换后得到

其中中间部分不就是协方差矩阵的定义吗？所以记为：

好，先到这里，我得喷一下网络上的PCA文章，很多文章说这里的Cov(x)就是X和X的转置相乘，我就想问问，是体育老师交的公式吗？什么时候协方差矩阵能这么简单就算出来了？问题是不知道谁带的头，导致网络上都是这么讲的，还一大堆文章前面原理也不说，含义也不讲一开始就讲协方差矩阵，有病吧？其实哪怕这里不是协方差矩阵，PCA照样成立，只不过很巧，这里就是协方差矩阵而且，并且从意义上讲，这里也就应该是协方差矩阵，因为我们的Var定义大家不觉得和协方差很像吗？如果说我们换了一种定义数据变化率的方式，得到的就不是协方差矩阵了，但是PCA原理照样成立，只不过公式换了而已。

协方差矩阵有很多有趣的性质，我也不细说了，可以自定去百科里看，总之协方差矩阵其实保证了后续我们进行坐标变化能够实现。

那么我们到这里就要找到n个W，因为W自身是基向量，那么必须是长度为1，而且n个W要相互正交。

也就是说我们要求||W||2=1且Var最大，那么就要用拉格朗日乘子法：

这个是第一个W的算式

对W求导得到：

两边同乘W的转置得到：

那么这就完美的符合了W是一个特征向量  α是一个特征值  而且α就是Var的结果，所以我们要用最大的特征值

对于第二个W

多了一个条件就是必须和第一个W正交，所以得到的拉格朗日乘子法的式子是：

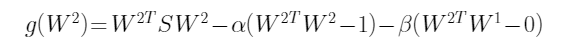
我之前故意不给W带上角标，怕大家搞混，现在必须带上角标了，因为第一个W已经求出来了

同理对W2求导，再化简，得到的也是W2是一个特征向量，新的特征值是第二大的特征值。

为此我们的PCA就结束了，我们就求出协方差矩阵的n个特征值对应的特征向量就是新的基向量了。

要降维？那就选前几个特征值最大的特征向量就可以了，想要几个就选几个。

那么在此，我发现生物中，用PCA去找特征基因的做法其实有问题，虽然主成分分解的确是叫做主成分分解，但是分解之后得到的是新坐标的坐标值，并不是原来的坐标。而基因一旦映射之后就不叫基因了，叫融合基因？所以我想换一个思路去做这个东西，如果有大佬知道这个PCA做特征基因筛选的确是有道理的能不能教我一下。