生物信息学之RMA(Robust Multi-Array Average)算法的背景校对过程
RMA算法是基因芯片数据预处理算法之中一个非常好用而且有效的方法。
本人最近正在学习这个算法,但是发现国内关于这方面的资料是真的很少。
RMA算法分为三个部分,
背景校对
归一化
最终计算表达强度
首先背景校对在Bioconductor包里是叫做preprocessCore的子包中实现的,有能力的同学可以自行下载源代码看,是用c语言写的,所以在R里面是不能直接看到实现的。(我看了一下,写的有点乱,尤其是注释,注释里有的函数的参数列表竟然和真正实现传入的不一样,我也是服了)
所以最后我没有看源代码,而是看了别人整理好的文章。所以我在这主要是做一个整理,方便大家能够看一篇文章就能把这个东西学明白了。
背景校对(background corret)
背景校对,顾名思义是消除背景噪音,在实现上采用了一个数学假设的方式,用概率公式进行消去的。
PMij=bgij + Sij 其中PMij是指在第i组数据中,第j号探针所观测到的数据,bg是指背景噪音,S是指真正的表达的信号
通过实验观察可设,S~Exp(λ) bg~N(μ,σ) S与bg为相互独立的 并定义B(PM)=E[S|PM] > 0 所求出的B也就是我们想要的背景校对的函数或者说算法。
首先,根据概率学内容,我们有 也就是标准正态分布的概率和概率密度的定义。
也就是标准正态分布的概率和概率密度的定义。
根据概率学的联合概率密度函数可得到
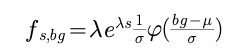
但是我们希望得到的是s关于PM的关系,而不是s和bg的关系,因此我们将bp用bp=PM-S替换,得到:
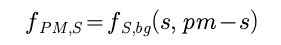 我在这里就不展开了,也没什么意义大家真的感兴趣可以自行展开
我在这里就不展开了,也没什么意义大家真的感兴趣可以自行展开
当然这个依旧不是我们所需要的东西我们真的想要的是S|PM时的概率密度,故得到如下式子:
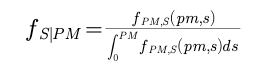 解释一下积分上下限为什么是0到pm因为我们假设s和bg都是大于0的,所以s小于pm大于0
解释一下积分上下限为什么是0到pm因为我们假设s和bg都是大于0的,所以s小于pm大于0
当然我就不展开了,这个展开之后大家凑成正态分布之后我直接给出最终的结果:
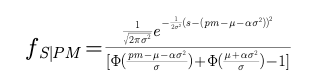 大家也能看出来这个化简过程应该是有点恶心的,这个公式编辑器实在难用,打出过程太累了。
大家也能看出来这个化简过程应该是有点恶心的,这个公式编辑器实在难用,打出过程太累了。
最后我们求积分便得到E(S|PM) 当然我也是直接给出最后结果了,为了方便表示我们规定了如下两个约定:
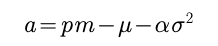 和
和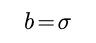
则最终结果: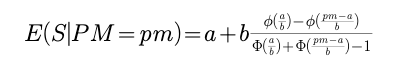
所以我们的问题便转化为求出三个概率的参数。
但是!!!我们发现根据参数估计我们只能得到如下两个式子
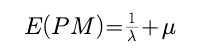
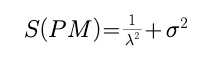
也就是说我们不可能通过参数估计得到最终的结果。
好吧,其实下面更难,我们的故事到这里还没得很结束。。。
为此我们引入非参数估计。非参数估计有很多做法,比如牛顿差值啊等等,这个百度上还是挺多的,因为统计分析在大多数专业都有用到。
不像生物信息学好难找资料。
在Bioconductor里面,使用的是一个叫做核函数估计的方法。
所以要先解释一下什么是核函数估计,这个网上也有资料,我这里就说一些重点。
核函数估计有一个前提假设是在我们的样本中出现的值其概率在统计学上是要比其他值高的。所以我们将每一个在样本中出现的值构建一个核函数K
核函数K有要求,他必须是一个概率密度函数。K有很多成熟的方案选择,我这里用正态分布举例。
我们假设以样本点x为中心其周围概率为 这个h如果是正态分布就是方差了,但在核函数里叫做平滑因子,用来控制在最后的结果是否光滑。核函数估计的作用就是将一些离散点的数据通过对每个点进行核函数的建立后,扩展到了连续的域上,任意点的最终概率为如下:
这个h如果是正态分布就是方差了,但在核函数里叫做平滑因子,用来控制在最后的结果是否光滑。核函数估计的作用就是将一些离散点的数据通过对每个点进行核函数的建立后,扩展到了连续的域上,任意点的最终概率为如下:
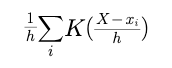 h的选择会很大的影响结果,在这里我们根据最小平方差的方式能得到一个最优h的取法,这个网上有教程,也不是我们现在要去了解的关键。
h的选择会很大的影响结果,在这里我们根据最小平方差的方式能得到一个最优h的取法,这个网上有教程,也不是我们现在要去了解的关键。
总之,我们根据核函数将我们输入的探针数据建立起了一个连续的图像。其图像的y轴为概率密度的叠加,图像的x轴为表达强度的观察值。
由于我们是假设PM=S+bg,S是满足指数分布的,指数分布的图像比较平滑,bg是满足正态分布的,正态分布有一个最大值。
所以在Bioconductor里面的做法就是将连续的拟合图像分成16384个采样点,看这么多采样点中哪个的概率密度叠加值最大,我们就有很大的理由相信这个x就是我们正态分布里面的μ。最后我们再带回原来的参数估计的两个式子得到另外两个参数。
现在我们三个参数都已经有了结果,显然问题就全解决了。至此我们完成了背景校验。。。。
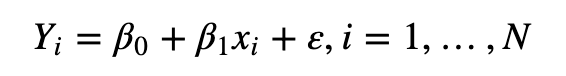


全部评论