Bioconductor包之中，有一个标准化方法叫做normalize.AffyBatch.contrasts()，这个方法参照的是一个2001和2003年Magnus Astrand写的两篇文章，其中2001年的文章并没有发表，而且现在网上找不到了。没办法只能强行读源码，所以我不敢保证我对于这个算法的理解是正确的。

首先，我需要翻译一下这个算法的中文意思，我个人觉得要叫做对比标准化比较合理。

这个算法的核心是选择一组参照组，对参照组进行loess回归，然后将原数据都在回归结果上进行映射然后得出最终的结果。所以参照组的选择就显得非常重要。

参照组选择的函数名叫做maffy.subset 这个函数的帮助文档是空的，参考的是Astrand M.在2001年的一个未发表的手稿，

这个函数我个人认为哈，有一些很奇怪的地方，我先简单说一下流程：

将原数据对每一行进行求平均值，也就是对某一个探针的所有组数据求平均

根据平均值排序（这里我就觉得很奇怪，毫无意义啊）

排完序后的原数据（注意不是平均数）按照列进行标号，原数据是某一探针检测到的表达值，根据表达值在这一列数据之中从大到小排第几号，就把这个号填入这个位置。

标完之后，每一行之中最大号减去最小号求出每一个探针在自己组里序号的大小之差，我们简称序号差。

引入一个变量prevn用于计算特定的分位点，然后求出前20%和后20%序号差中的这个分位点值，并除以总探针数(n)，分别用left和right表示这两个分位点的值。

然后若第i位序号差小于n*left + i*(right-left)，则选出来，当做新的subset

重复进行4，5，6直到这个subset的大小满足要求为止，默认是5000，并且允许有一定的误差，同时默认迭代100次，如果还是没找到则报错。

其中prevn的值根据subset是大于要求的数量还是小于要求的数量会适当的变大和变小，来控制分为点位置，以控制subset大小。

从这个过程可以得出subset所取出来的值是序号差比较小的5000个，因为序号差小，就说明这个探针相对于其他探针是比较稳定的，也就是这部分数据更具有可信度。(我就不明白了，直接按照序号差进行排序再取出前5000个显然会快很多吧，或者直接取出前6000个再进行随机取5000个，这都是很快的算法，相反的，这个不断重复计算序号差和分位点是非常大的运算量吧。因为没找到原稿，也搞不清这个过程的数学分析是什么原理，反正看源码我是很懵逼的，觉得做了很多无用功，当然这都是我个人主观臆测)

subset的选择可以根据参数选择只在pm中选，还是mm中选，还是pm和mm一起，以及先对pm选在对mm选。

找到subset之后，进行正式的归一化过程。归一化过程将第一组作为x其他组作为y

这里我们一定要记住我们做的是标准化，也就是消除组间的差异，具体意义可以看我前几篇文章，已经举例说明了标准化的意义。

之后再对所有数据包括subset进行log处理，当然也可以不处理，可以根据参数选择。这个过程是减少组间大小的距离，例如1000和10经过log之后就变成3和2了。

如果数据本身就没有很大的突变，其实无需log，当然log了也没什么问题，因为后面会e回来。

接下来是对数据按照transmat矩阵进行映射，这个矩阵是由n个无关向量组成，其组成方式如下（注意这里只是一个构建transmat的方式，并不是唯一的）：

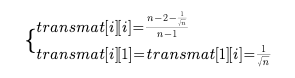其他位置全都用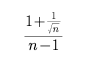填充

可见这个矩阵是一个正交矩阵，正交矩阵有一个性质，就是正交矩阵的转置就是他的逆矩阵。而且正交矩阵的意义是让某一组的探针减去其他组的探针，使得原数据经过正交矩阵之后每个位置变成了该组该探针同其他组的对比度，也就是差异，也就是我们这个算法叫做constrast的本质所在。

就是我们希望这个对比度能变成0，至于为什么我们要求出subset，是因为使用为loess算法复杂度太高了，选择一个小的集合当做参考组能够减少计算复杂度。

同时我们将subset的第一列作为自变量，其他列作为因变量，这样就得到了一个从原数据到差异值的简单模型。

「根据论文里的还有个很简单的结论，

假设我们有两个transmat矩阵M1和M2，有：

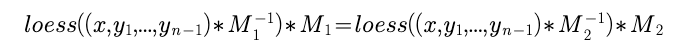
显然是成立的，因为映射回来再映射回去的结果肯定是相同的，所以M是有无数种取法的，并不唯一。」

然后对subset进行loess回归，这个回归网上有一些简单的介绍，我就不多说了。

我们设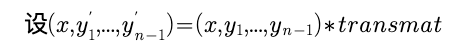其中的y’就是我们的对比值了，我们先进行一次loess回归，

这个回归的意义是让这个对比值平滑一些。

因此我们得到了x到y’的映射，我们希望的是y'到0的映射，因为我们希望y‘是0，目的就是将对比值尽可能小吗，这样才叫标准化。

接下来：

我们再进行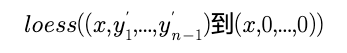的变化，也就是将原数据的对比度映射到对比度是0的数据上去，

之后将原数据再这个拟合上进行预测。

然后至此我们就将数据拟合到了一个尽可能没有组间差异的数据上，也就是使得组间对比度为0。从而完成了我们的标准化。

ps.

    我觉得很奇怪的地方就是这个基准线并不能肯定是准确的吧，要是基准线是错的，那不是整体都废了。

之后loess后的数据再加上最大值最小值后再loess一次，然后对原数据进行预测后作为最终结果，我个人觉得原因是加上一些不变量，能够让loess的回归结果更加平滑，因为loess之间那个w权重因为维度大了，反而变小了。

另外，这个算法，其实我不敢说我真的理解了，因为我觉得loess过程是一个很不可控的算法，有可能过拟合也可能欠拟合，没法说这个算法真的具有多大的意义，我个人觉得没之前的算法稳定，我只能说只是理解了一个大概吧，一些简单过程。

但是这个算法正是因为稳定性不够，所以要求原数据要先做完背景校正，不然一些突变的结果可能会导致数据出现很大的偏差，尤其是这些突变结果出现在了subset里面，更别说出现在subset的第一组里时，当然在选取subset时已经是选出的5000组序号差最小的组了，可以说已经考虑了这些问题了，但还是需要数据尽可能消去背景。